

Discover more from According to Sci-Faith
Multiverse, Hidden Variables or Random Chance?
Which interpretation of quantum mechanics describes reality?
The following is an article that originally appeared in the "Studium Integrale Journal" (Jahrgang 30 Heft 1) of the Studiengemeinschaft Wort und Wissen.
Quantum mechanics is considered one of the best confirmed theories. Nevertheless, it continues to puzzle scientists. Even almost 100 years after its formulation, there is still disagreement about how its statements should be interpreted. There are many interpretations, all of which are consistent with the scientific data. This multitude of equally valid interpretations of the same theory leads us to a surprising analogy with world views.
Abstract
The double-slit experiment shows that quantum objects have both wave and particle properties (wave-particle duality). In addition, the type of the measurement has an influence on the outcome of the experiment (measurement problem). Mathematically, these observations can be described using various approaches, e.g. the Schrödinger picture, the Heisenberg picture and Feynman's path integral formulation. According to the Schrödinger picture, the quantum objects are in a superposition of several states and are only fixed to one state by the measurement.
The probability with which they are measured in a given state can be determined from Schrödinger's wave equation.
The interpretation of these equations is the subject of controversial debate and it has been shown that they can be interpreted in different ways. The most common is the Copenhagen interpretation, which states that nature actually behaves in this way. The measurement problem therefore shows the limit of what science can describe.
The De Broglie-Bohm theory assumes that there are additional hidden variables that determine the state of the particles. These move on a pilot wave given by the Schrödinger equation.
In the many-worlds theory, every state is assumed after a measurement, only not in the same universe. Each measurement here requires the creation of many new worlds, in each of which one of the possible states is assumed.
Despite their differences, all these interpretations can conclusively explain the double-slit experiment.
Similarly, many natural phenomena can also be explained both by naturalistic evolution as well as supernatural creation.
Introduction
At the end of the 19th century, many scientists were of the opinion that the open questions of physics would soon be solved. Physics would soon be completed. For this reason, Max Planck was advised not to study physics (Planck 1943).
Today we know that this was far from the was far from the truth. The 20th century began with a downright explosion of new discoveries and the resulting subfields within physics. On the one hand, Albert Einstein's special theory of relativity in 1905 revolutionized our understanding of space and time (Einstein 1905). Later Einstein developed the more general form of the theory of relativity, which includes gravity (Einstein 1915). On the other hand the same Max Planck with his description of blackbody radiation laid the foundation for quantum mechanics (Planck 1901).
The blackbody problem was one of the open questions in physics.
A blackbody is an idealized construct that absorbs any radiation that hits it.
According to the laws of radiation theory, this means that it emits all the radiation that it produces due to its temperature. Our sun, for example, can be approximately regarded as such a black body.
If you try to use the classical laws of radiation to calculate what intensity of the light is emitted by the blackbody at a given temperature and frequency, the result is that it tends towards infinity at high (ultraviolet) frequencies.
Such a solution not only makes no physical sense, but also contradicts the measurement results.
After all an oven or a light bulb does not emit large amounts of ultraviolet light. Also, the spectrum of light from the sun has a comparatively low UV content. This problem was known as the "ultraviolet catastrophe".
Planck was able to solve it by introducing an auxiliary constant known today as Planck's constant. Originally, he intended to cancel this at the end of his calculations. However, he only obtained results with a non-vanishing Planck constant. This means that energy does not occur in arbitrary quantities, but in quantized packets of fixed size. This realization gave rise to the concept of quantum mechanics.
Even more than the theory of relativity, quantum theory has put the imagination and understanding of scientists to the test.
Further discoveries, such as the photoelectric effect, showed that light not only acts as a wave, as was previously assumed, but also has the properties of particles.
Newton had already suspected this. Conversely, it was shown that objects previously regarded as pure particles, such as electrons, also have a wave nature.
Even more than the theory of relativity, quantum theory has put the imagination and understanding of scientists to the test.
This situation became even stranger when it was discovered that the measurement itself has an influence on whether the measured object behaves like a particle or like a wave.
This phenomenon, which contains the essential statements of quantum mechanics, is particularly easy to illustrate using the double-slit experiment.
The Double-Slit Experiment
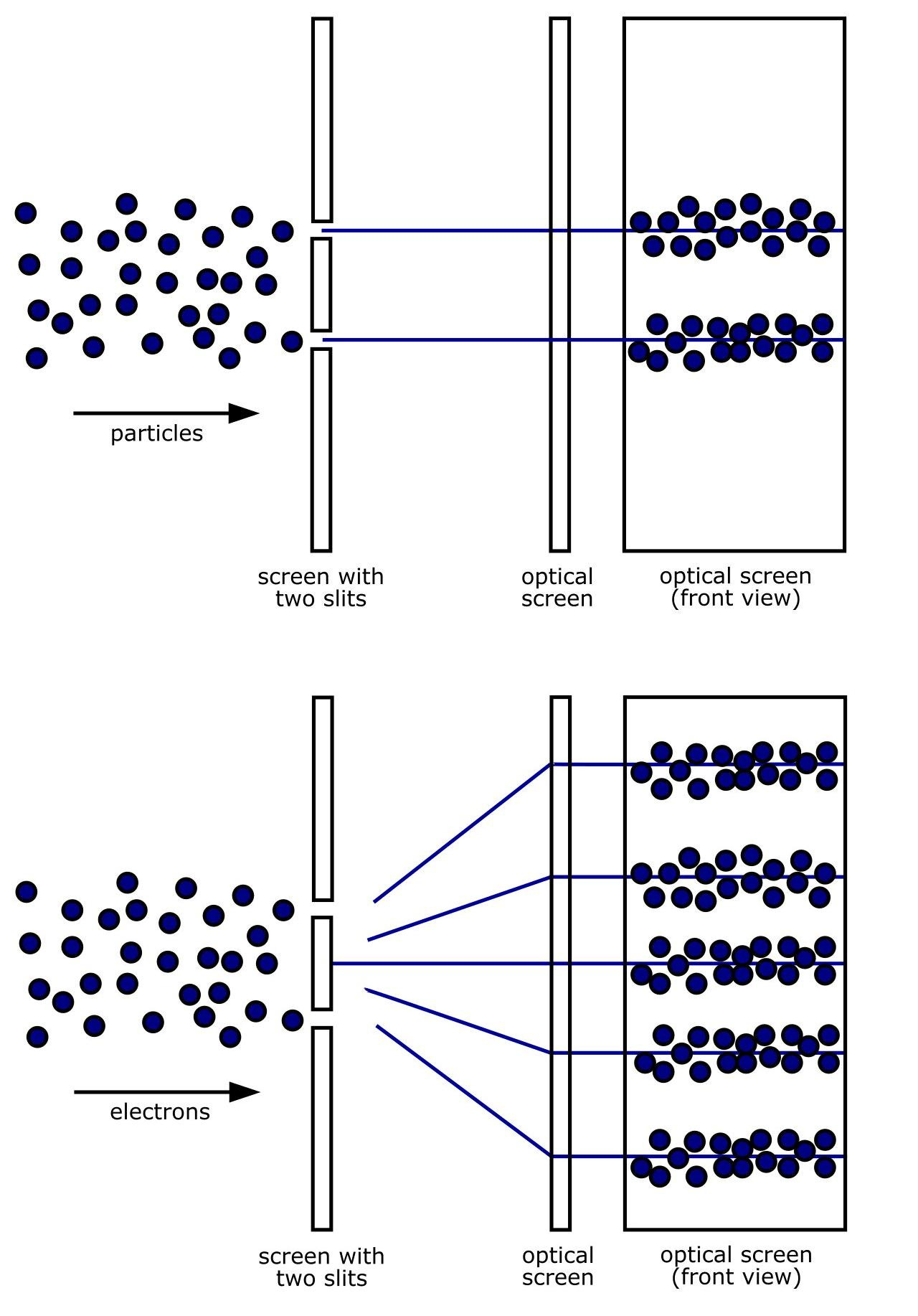
The structure of the double-slit experiment consists of two walls: The front wall is provided with two slits. The rear wall resembles a screen that absorbs incoming objects. Such an experimental setup is interesting because particle and wave objects behave differently here. It can be used to determine whether objects such as light behave like a wave or a particle.
With particle-like objects, the behavior is simple: the particles that do not bounce off the front wall will pass through one of the two slits and therefore also arrive in the area around these two slits on the rear wall (cf. Fig. 1).
With wave-like particles, the behavior is more complicated: a wave will, after passing the double slit, split into two waves (one per slit). These meet again behind the double slit. Here two effects can occur in principle:
On the one hand, a wave trough can meet a wave trough or a wave crest can meet a wave crest.
On the other hand, a wave crest can meet a wave trough or a wave trough can meet a wave crest. The result is the sum of the amplitudes of the waves hitting each other. This means that in the former case, the amplitude will double, while the amplitudes cancel each other out in the latter case. This has a pattern with a large maximum in the center, followed by smaller maxima towards the outside. This effect is called interference and the resulting pattern is called an interference pattern (cf. Fig. 1).
We now execute this experiment with photons or electrons, for example. It results in an interference pattern in both cases. Problem solved, we are dealing with waves, you might think. But if you turn down the intensity of the radiation, you notice that individual points are always detected on the screen, which in turn indicates a particle nature. This seems contradictory. How can an object act simultaneously as a particle and as a wave? It is as if the particle passes through both slits, interferes with itself and then hits the screen. The question is what exactly happens at the double slit. Therefore, we now position a detector at the front wall, which checks which slit the particle goes through.
And this is where it gets strange: if we measure which slit the object passes through, we know that it will only go through one slit or the other.
At the same time, an interference pattern no longer appears on the screen, but the pattern that would have been expected in the case of particles. In other words, by measuring which slit the object passes through, we have changed the outcome of the experiment, as if the objects knew that we were observing them and would therefore behave differently. This effect is called the measurement problem.
Mathematical Description
Even though the new findings were very strange and, as we will see later, no satisfactory interpretation has yet been found, a mathematical description was discovered relatively quickly:
In 1925/26, Erwin Schrödinger with his wave mechanics (Schrödinger 1926) and Werner Heisenberg with his matrix mechanics (Heisenberg 1925) independently found a suitable description of the effects. Schrödinger established the wave equation named after him, which can describe the wave behavior of quantum objects at any point in time.
However, an interpretation had to be found had to be found as to what this wave physically describes. Max Born interpreted it such that the magnitude squared of the wave function indicates the probability of finding a particle in a certain state.
Quantum mechanics therefore works in such that quantum objects are in a superposition of several different states.
During a measurement, however, the object is always always found in a single state. The wave function is a measure of the probability of finding a quantum object in a certain state at a certain time. Since a measurement cancels the superposition, this is referred to as the collapse of the wave function.
With this description it is possible to describe the behavior on a microscopic level. However, this is not completely possible: only probabilities can be given as to whether something will happen or not.
In classical physics, i.e. physics without quantum mechanics, if the initial conditions of an object and the forces at work are known, you can predict their behavior definitely and at any point in time.
This is no longer possible in quantum mechanics.
Quantum mechanics is therefore not deterministic. One of the questions that arises is whether this means that quantum mechanics is an incomplete theory or whether nature actually behaves in this way and the processes at a fundamental level are left to chance.
Before we pursue this question, it should be mentioned that there are various mathematical descriptions of quantum mechanics.
In addition to the Schrödinger picture described before there is the Heisenberg picture, which is similar and which can be converted into the Schrödinger picture through a mathematical transformation. In addition, Richard Feynman developed the so-called path integral formulation of quantum mechanics in his doctoral thesis (Feynman 1948). In classical physics (physics without quantum mechanics) an object chooses the path on which the action (defined as energy times time) is minimized. In Feynman's path integral formalism, every possible path that an object can choose contributes to the total probability that it will move from A to B. The smaller the action of the respective path from A to B, the higher the is the contribution to the overall probability.
This formulation is also equivalent to the other descriptions and can be derived from them.
Various Interpretations
Since its formulation, quantum mechanics has been the subject of controversial debate. Its usefulness was undeniable. Even today it is considered one of the best confirmed theories. However, many of its statements, such as indeterminism, were and still are a thorn in the side of many scientists.
This was also the case for Albert Einstein, who used the words "God does not play dice" to express his displeasure with quantum mechanics, which is based on probabilities (Einstein & Born 1972). After a mathematical description of quantum mechanics was found, we came to the actual problem of interpreting these findings appropriately. No conclusive result has yet been achieved in this area. This is also due to the fact that the same predictions can be determined from each of the different interpretations and the "correct" interpretation can therefore only be tested experimentally to a limited extent.
The most common interpretations are briefly described below.
The Copenhagen Interpretation

The first interpretation, known as the Copenhagen was initially formulated as early as 1927 by Niels Bohr and Werner Heisenberg (see Fig. 2). In principle, it states that the phenomena of quantum mechanics do not indicate an incompleteness of the theory, but rather exist in nature. They therefore show where the limits of science lie:
Only that which is measured is real. No statement can be made about events that occur between the measurements without getting caught up in contradictions.
This can be seen, for example, in the double slit described above:
If you look at what happens before the measurement on the screen, it is to be expected that about one half of the half of the objects hitting the screen through the first slit and the other half through the second slit. Summing up the expected distributions, a pattern is obtained that does not correspond to the interference pattern (cf. Heisenberg 1979).
In science, something objective that is independent of the observer becomes something subjective that has no clearly definable reality beyond our measurements.
What happens between the measurements cannot be answered. With the wave function quantum mechanics provides a tool to describe what could happen. This can be used to determine the probability of what future measurements will reveal. But only what is measured can be certain. Thus in science, something objective which is independent of the observer becomes something subjective that has no clearly definable reality beyond our measurements.
In physics, this interpretation is regarded as the standard. This is mainly because it is pragmatic and argues according to the principle "that's just the way it is". This is helpful in order to focus on scientific work without getting lost in endless philosophical quandaries. This view of the theory of quantum mechanics as a tool without a deeper reality can be classified as instrumentalism. In contrast to this is scientific realism, which assumes that reality is as predicted by our confirmed theories.
Nevertheless, the Copenhagen interpretation can also be regarded as a real description of reality.
Still, many scientists are dissatisfied with this interpretation and especially the resulting indeterminism, which is also due to the fact that until the advent of quantum mechanics, every theory made deterministic predictions. Therefore, over the course of time alternative interpretations were developed.
Hidden Variable Theories
Hidden-variable theories are an umbrella term for interpretations of quantum mechanics which assume that quantum mechanics is not a complete theory and further (hidden) variables exist that determine the system. If such a such a theory uses local hidden variables, it would it would fulfill Bell's inequalities (Shimony 2004).
It was experimentally confirmed, however, that these inequalities are not fulfilled (Aspect 1999). Theories with hidden variables are thus variables are severely restricted.
De Broglie-Bohm theory: The best-known non-local theory with hidden variables, and therefore not affected by these restrictions, is the De Broglie-Bohm theory (see Fig. 3). It states that the Schrödinger equation does not describe the entire system. According to this theory, each particle has a well-defined location and a well-defined velocity, which are determined by a by a so-called guiding equation. The wave function then acts as a guiding wave (pilot wave).
Since the guiding equations are determined from a differential equation of the wave equation initial conditions must be found for an exact description. Since these cannot be determined, this leads to the apparent indeterminism of quantum mechanics (Dürr, Goldstein & Zanghí 1992).

Many-Worlds Interpretation
The many-worlds interpretation is probably the best known. This avoids the problem of indeterminism and the measurement problem by assuming that the Schrödinger equation is suitable for describing any closed system (Tegmark 2009). This means that at any point in time, even during a measurement, the system can be completely described with the Schrödinger equation. Conversely, this means that there can be no collapse of the wave function and instead, after a measurement of a superposition state, all states are assumed, but in different universes (see Fig. 4).
With each measurement process, there is for each possible outcome a new branch of a universe in which exactly this outcome has occurred.
The idea of several universes in which one's own self exists again and has taken a different path is very interesting for many people.
This concept of a multiverse has now reached pop culture and can be found in many books and films.
The idea of several universes in which one's own self exists again and has taken a different path is very interesting for many people. Whether reality really looks like this is unclear due to the sheer number of conceivable universes, which in most cases are like two peas in a pod.
This is just an overview of the many interpretations of quantum mechanics that have been developed since its formulation. They are all able to reproduce the results of quantum mechanics. This means that it is not possible to find out scientifically which is the correct interpretation.
It may be possible at some point in the future to use more precise measurement to exclude one or the other interpretation. However, it is quite possible that further interpretations will be found in the meantime. Presumably one will never be able to decide which interpretation is the correct one using scientific methods alone. This shows the limits of science: When it comes to interpreting scientific findings, the scientific method can only provide limited answers.
Other means must be used here.
And even if you arrive at a reasonable interpretation that is consistent with the measurement data, this does not mean that it is the right one. There could be another interpretation that describes the measurement data just as well or even more accurately.
Even if you arrive at a reasonable interpretation that is consistent with the measurement data, this does not mean that it is the correct one.
One other thing stands out when considering of these different interpretations:
Although the statements of quantum mechanics are not deterministic, as can be seen from the Copenhagen interpretation, most alternative interpretations allow for a deterministic world view.
In a deterministic view of the world, everything is predetermined, even the processes in the human brain. Free will (in the sense of genuine libertarian freedom) does not exist according to this view.
Furthermore, the many-worlds interpretation results in a view according to which each individual human being is nothing special, but only one of countless other variants of "his" life and basically only an arbitrarily short episode of a gigantic copying process. Decisions made would not represent anything worthy of recognition, since it would be pure coincidence that "one" would find oneself in a universe in which "one" would have made these decisions. What is more:
The personal identity of the human subject - that I am the same, throughout time and thus through very many events of my life - becomes questionable here.
These interpretations obviously stem from a fatalistic view of the world, which also denies the objective personal identity of the ego, as it corresponds to our natural understanding of ourselves. This does not follow from scientific data; after all, the Copenhagen interpretation is also in harmony with this data. Rather, it stems from the personal world view of those who postulated these postulated these theories.
For the sake of completeness, it should be said that there are some interpretations besides the Copenhagen interpretation that do not contradict an indeterministic world view. The Free will theorem by John Conway, for example, even goes so far as to assign a degree of free will to particles under certain conditions (Conway & Kochen 2006).

Different World Views
This situation of different, empirically equivalent interpretations of a theory cannot only be applied to individual scientific theories, but also to the interpretation of science as a whole. This is often referred to as different world views.
If we replace the findings and interpretations of quantum mechanics with those of science as a whole in our considerations, we essentially arrive at the same statement.
On the one hand, there are the scientific facts (i.e. the pure measurement data), which are irrefutable within their respective uncertainties. On the other hand, there is an interpretation of these facts.
This can be strongly influenced by one's own world view. The more relevant these facts are for the decisive questions of our worldviews, the more this is the case. In this respect, it is hardly surprising that, as already stated, a fatalistic and deterministic worldview can be found in most theories, considering that many scientists share such a worldview. However, it is not so much the scientific facts that lead to such a world view but rather it is the presence of such a worldview among researchers that leads to such an interpretation of the facts. The multiplicity of different interpretations of quantum mechanics thus represents an analogy to the multiplicity of different worldviews, which are in line with the scientific data.
It is not so much the scientific facts that lead to such a worldview, but rather the worldview that leads to a particular interpretation of the facts.
Conversely, this means that it should be possible to find interpretations of scientific facts that are in harmony with other worldviews.
It is also to be expected that the correct worldview yields an interpretation of the facts that goes beyond the current theories and leads to further (empirically sound) statements that can be used to confirm it.
The reason why the Copenhagen interpretation is still considered the standard is that none of the alternative interpretations provide any added value in scientific terms. In the same way, alternative theories cannot be expected to replace the existing theories as long as they do not make more accurate predictions than these, which can then be tested experimentally.
In summary, this situation of different, empirically equivalent interpretations of quantum mechanics shows once again that there are several ways of interpreting the facts in science.
The predominance of one interpretation does not necessarily mean that this interpretation, let alone the world view on which it is based, is the correct one. Just as it is impossible to scientifically arrive at a unambiguous interpretation of quantum mechanics it is scientifically impossible to refute the world view of a created or randomly created world. This is beyond the limits of science.
It is only possible to choose a provisional interpretation that best does justice to the findings as a whole.
Literatur
Aspect A (1999) Bell’s inequality test: more ideal than ever. Nature 398, 189–190. doi:10.1038/18296.
Conway J & Kochen S (2006) The Free Will Theorem, Found. Phys. 36, 1441–1473. doi:10.1007/s10701-006-9068-6.
Dürr D, Goldstein S & Zanghí N (1992) Quantum equilibrium and the origin of absolute uncertainty. J. Stat. Phys. 67, 843–907, doi:1007/BF01049004.
Einstein A (1905) Zur Elektrodynamik bewegter Körper. Annalen der Physik und Chemie, 17, 891–921.
Einstein A (1915) Erklärung der Perihelbewegung des Merkur aus der allgemeinen Relativitätstheorie, Sitzungsberichte der Preußischen Akademie der Wissenschaften, 831–839.
Einstein A & Born M (1972) Briefwechsel 1916–1955. Rowohlt Taschenbuchverlag, Reinbek bei Hamburg, 97f.
Feynman R (1948) Space-time approach to non-relativistic quantum mechanics. Rev. Mod. Phys. 20, 367–387.
Heisenberg W (1925) Über quantentheoretische Umdeutung kinematischer und mechanischer Beziehungen. Zeitschrift für Physik 33, 879–893. doi:10.1007/BF01328377.
Heisenberg W (1979) Quantentheorie und Philosophie. Reclam, S. 55–56.
Planck M (1901) Ueber das Gesetz der Energieverteilung im Normalspectrum. Annalen der Physik 309, 3, 553–563. doi:10.1002/andp.19013090310.
Planck M (1943) Wege zur Physikalischen Erkenntnis, Reden und Vorträge, 1. Leipzig, S. Hirzel.
Schrödinger E (1926) Quantisierung als Eigenwertproblem. Annalen der Physik 79, 361, 489; 80, 437 und 81, 109.
Shimony A (2004) Bell’s Theorem. In: Zalta EN: The Stanford Encyclopedia of Philosophy, Stanford.
Struyve W (2004) The De Broglie-Bohm pilot-wave interpretation of quantum theory. arXiv:quant-ph/0506243.
Tegmark M (2009) Many Worlds in Context. arXiv:0905.2182.
Subscribe to According to Sci-Faith
The Compatibility of Faith and Science





